产品报价分类
产品技术参数
大型冷却塔
大型冷却塔热力计算模型
发布时间:2015-03-09 18:17:34 来源: 浏览次数: 关键词:冷却塔,热力,模型
这是默认内容
摘要:基于质量守恒和能量守恒原理,以出塔水温作为冷却塔冷却性能的评价指标,建立了大型冷
却塔热力计算的湿差模型,并与目前常用的焓差模型以及四变量模型进行了比较,分析了不同模型的计算结果差异以及气象条件(如大气压力、干球温度及湿球温度)、淋水面积和风速等参数对冷却塔出塔水温的影响.即随着干球温度及湿球温度的降低,或者在一定的范围内,淋水面积的增大,或者风速的增大,出塔水温均会降低.结果表明:湿差模型和焓差三阶模型是适用于大型或超大型冷却塔的热力计算模型,在大型冷却塔设计时,应特别重视循环冷却水系统冷端参数的综合优化分析.关键词:大型冷却塔;热力计算;出塔水温;湿差模型;焓差模型;四变量模型中图分类号:TK123 文献标识码:A 文章编号:1000Ο1980(2009)05Ο0591Ο05冷却塔是火电厂的重要冷端设备之一,其冷却性能的好坏直接影响整个电厂运行的经济性和安全性.而冷
却塔的出塔水温是衡量冷却塔冷却性能的重要技术指标[1Ο4]
.根据冷却塔的出塔水温及其变化规律,不仅可以对冷却塔系统进行运行监控和状态优化分析,而且可以为冷却塔的运行维护和检修改造提供基本技术依据.
冷却塔的出塔水温对发电机组热效率的影响较大,如对于1台超高压汽轮机,当冷却塔出塔水温降低1℃,凝汽器真空提高270Pa,机组热循环效率提高012%~013%[5],因此,在冷却塔设计时首先必须采用准
确的热力计算模型.
在现行的冷却塔设计中,大多采用以麦克尔方程[6]为基础的焓差模型,即将接触散热和蒸发散热相关的2个未知变量(不同高度淋水截面的空气干球温度和空气中的水蒸气分压力)均用1个未知量“比焓”来代替进行热力计算,而很少用不同传质和传质系数的计算模型来计算.在焓差模型的求解上,则大多采用辛普森二阶积分法.但工程实践表明,这种以辛普森二阶积分的焓差模型(以下简称焓差二阶模型)不能准确地适用于目前的大型冷却塔[7](8500m2≤A<11000m2)以及超大型冷却塔(A≥11000m2)的热力计算分析,其中A为淋水面积.本文基于质量守恒和能量守恒原理,建立了适用于大型冷却塔热力计算的新的湿差模型,并与焓差二阶、三阶模型以及四变量模型分别进行了比较计算,分析了各有关参数对大型冷却塔出塔水温的影响.
1 湿差模型的推导
1.1 水体质量守恒方程
根据质量守恒原理,水面蒸发的水量,即部分变为空气中水蒸气的水量可表示为
dQ=βpv(p′v-pv)dV
(1)
式中:Q———进入冷却塔的水量,kg/s;V———填料体积,m3;βpv———单位填料体积与水蒸气压力相关的散质系数,kg/(m3・Pa・s);p′v———空气温度为水温t时的饱和水蒸气压力,Pa;pv———水蒸气的分压力,Pa.p′v,pv可
分别改写为
p′v=x′x′+01622pa
(2)pv=
xx+01622
pa
(3)
式中:x′———空气温度为水温t时的饱和蒸气含湿量,kg/kg;x———空气中水蒸气的含湿量,kg/kg;pa———大气压力,Pa.
将式(2)~(3)代入式(1),得
dQ=βxv(x′-x)dV=βxv(x′
-x)Adz(4)βxv=1161βpv[1-1161(x′
+x)]pa(5)
式中:βxv—
——单位填料体积与空气含湿量相关的散质系数,kg/(m3・s);A———塔中填料水平断面面积,m2;z———垂向坐标,向上为正.
由于空气中水蒸气增加的水量dQ也可以表示为
dQ=Gdx
(6)因此,由式(4),(6)可得
βxv(x′-x)Adz=Gdx(7)式中G为进塔空气质量,kg/s.
1.2 热量平衡方程
水散出的总热量为其水面接触散热量与其蒸发水量所引起空气温度增加的蒸发散热量的总和,即
dHq=αv(t-θ)Adz+γwβxv(x′
-x)Adz+ctdQ(8)
式中:Hq———水散出的热量,kJ/s;αv—
——单位体积接触散热系数,kJ/(m3・s・℃);t———水温,℃;θ———空气的干球温度,℃;γw—
——水的汽化热,取242813kJ/kg;c———水的比热容,取411868kJ/(kg・℃).空气增加的总热量为
dHg=Gcwdθ+hqdQ(9)式中:Hg———空气增加的热量,kJ/s;cw———湿空气的比热,取1105kJ/(kg・℃);hq———水蒸气含热量,kJ/kg.
在正常稳定运行状态下,水散发的总热量等于空气增加的总热量,则由式(8),(9)可得
αv(t-θ)Adz+γwβxv(x′
-x)Adz+ctdQ=Gcwdθ+hqdQ(10)考虑到蒸发水量dQ相对很小,将其带走的热量忽略,且hq=r0+cvθ,则式(10)可化简为
Gcwdθ=αv(t-θ
)Adz(11)
式中:r0———水0℃时的汽化热,kJ/kg;cv———水蒸气比热容,取11842kJ/(kg・℃
).1.3 热传递平衡方程
水损失的热量为
dHq=cQt-c(Q-dQ)(t-dt)
(12)式(12)为忽略二阶微小量化简得到的.将式(8)代入式(12),化简后可得
cQdt=αv(t-θ)Adz+γwβxv(x′-x)Adz(13)
令
GA=ga,Q
A
=q,将式(7),(11),(13)分别改写导出湿差模型即可:dxdz=βxv(x′-x)ga
(14)dθdz=α
v(t-θ)cwga
(15)dtdz=αv(t-θ)+γwβxv(x′-x)cq
(16)
求解式(14)~式(16)需作如下假设:(a)系数αv,cv,cw,c及γw都取常数;(b)水温取其断面平均值,不考虑交面阻力;(c)空气在填料出口处未达到饱和状态;(d)填料面积沿垂直方向不变;(e)取刘易斯数Le=
αv/(cwβxv)=111,1,0193,0191,019,分别计算其对出塔水温的影响.
2 焓差模型和四变量模型简介
2.1 焓差模型
水所损失的热量等于空气所获得的热量,即
cqdt=gadi
(17)
式中i为湿空气焓,kJ/kg.
从水到空气的热量传递,可用焓差[8]表示为
cqdt=βxv(i′
-i)dz(18)
式中i′为水温t时的饱和空气焓,kJ/kg.
将式(18)改写成积分形式,即
βxvz
q
=
∫
t1
t2
cdt
i′-i
(19)
求解式(19)需作如下假设:(a)水膜或水滴的表面温度与冷却水内部温度一致;(b)忽略蒸发水量损失;
(c)由于冷却塔内水蒸气的压力很小,对塔内压力影响很小,因此按照平均大气压来计算;(d)散热系数、散质系数和湿空气的比热在整个过程中均为常数.
对于式(19)右边项的积分,可采用辛普森展开法.当取辛普森阶数n=2,3时,可分别写成式(20),(21)的积分形式,本文分别称之为焓差二阶、三阶模型,即
∫
t1t2cdt
i′
-i=
cwΔt3n1h′2-h1+4h′m-hm+1h′1-h2(20)∫
t1
t2
cdt
i′-i=
cwΔt3n
1
h′2-h1
+
4
h′23-h13
+
2
h′13-h23
+
1
h′1-h2
(21)
式中:h1,h2———进塔、出塔空气比焓,kJ/kg;hm,h′m———塔内平均水温的空气比焓、饱和比焓;h13,h′23———空气干球温度为t=t2+1/3Δt时的比焓、饱和比焓,kJ/kg;h23,h′13———空气干球温度t=t2+2/3Δt时的比焓、饱和比焓,kJ/kg.2.2 四变量模型
根据质量守恒和能量守恒原理,并考虑蒸发损失引起的水量变化,可得四变量模型[6]:
dq
dz
=βpv(p′v-pv)(22)dt
dz=αvcq(t-θ)+γwβpvcq(p′v-pv)(23)dθdz=ccwgaqdtdz+1c(ct-γw-cθ)dq
dz
(24)dpv
dz=(pa-pv)201622gapadqdz
(25)
求解四变量模型需作如下假设[9]:(a)冷却塔内水蒸气分压力所占比例很小,可采用不变的大气压力;
(b)系数αv,cv,cw,c及γw都取常数;(c)水温取其断面平均值,不考虑交面阻力;(d)空气在填料出口处未达到饱和状态;(e)填料面积沿垂直方向不变.
3 4种模型的比较计算分析
现针对湿差模型、焓差二阶模型、焓差三阶模型、四变量模型这4种热力计算模型进行比较计算分析,并作如下说明:(a)湿差模型的求解,采用中心差分方法将偏微分方程组转化为差分方程组后再编写程序;(b)焓差模型的求解,分别对其二阶、三阶模型进行对比分析,同时为了保证式(20)的解有合理的求解区间曲
线[10],根据4个焓差都大于零的条件来编写Fortran程序,以使其解具有数学和实际意义;(c)四变量模型,采用中心差分方法将其转化为方程组后再进行求解,并考虑水量的蒸发损失.
本文以邯峰电厂冷却塔为研究对象.该冷却塔为自然通风冷却塔,淋水面积为9000m2,采用高为112m的T26Ο60°梯形波填料.气象条件为:空气干球温度2115℃,湿球温度17℃,大气压力99850Pa.
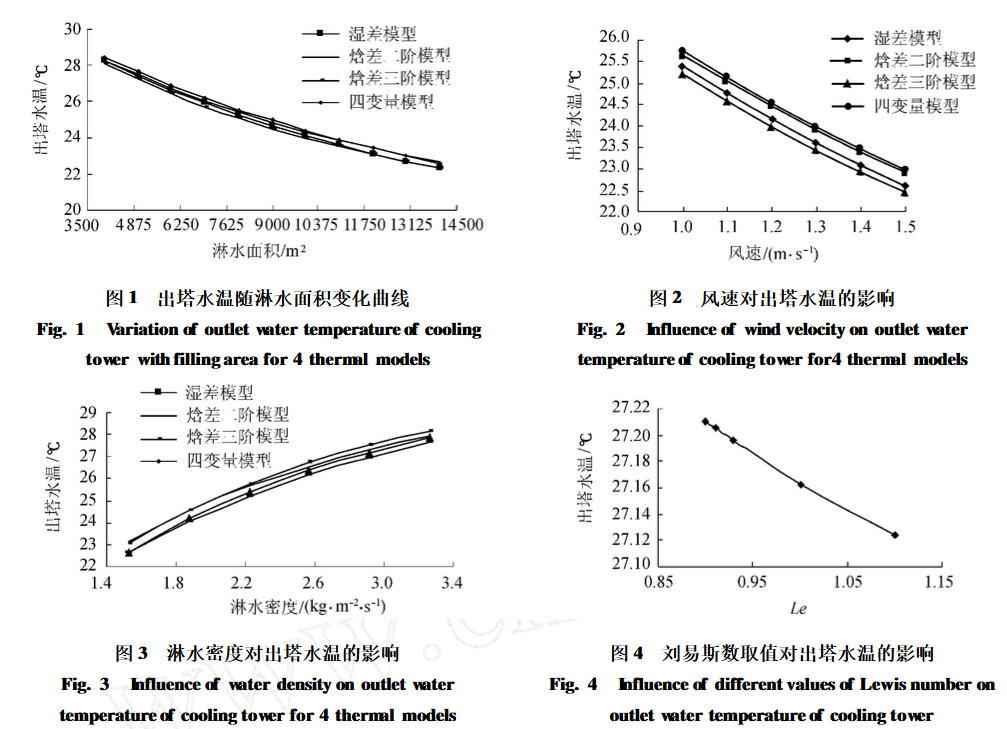
4种模型的热力计算结果如图1~4所示.比较分析这些计算结果,可得出如下结论:
a.四变量模型的出塔水温计算结果比其他模型大,与实测出塔水温比较误差较大,说明该模型相对不
准确.
b.由图1可见,当淋水面积从4000m2增大到8000m2时,焓差二阶模型的出塔水温计算结果与湿差模型的计算结果相差很小.但随着淋水面积的增大,焓差二阶模型的计算结果与湿差模型的计算结果相差越来
越大,此时,焓差三阶模型与湿差模型的计算结果越来越接近,且与实测出塔水温很接近.说明大型冷却塔的热力计算不宜再用焓差二阶模型,应采用湿差模型和焓差三阶模型.
c.由图2可见,随着风速的增加,出塔水温呈近似直线下降趋势.而由图3可见,随着冷却塔淋水密度的增加,出塔水温也相应增加.由图4可见:随着刘易斯数的增大,出塔水温减小;当刘易斯数从111减小到110时,出塔水温增加0115%.由此可见,刘易斯数的选取是值得注意的问题

大型冷却塔热力计算模型

摘要:基于质量守恒和能量守恒原理,以出塔水温作为冷却塔冷却性能的评价指标,建立了大型冷
却塔热力计算的湿差模型,并与目前常用的焓差模型以及四变量模型进行了比较,分析了不同模型的计算结果差异以及气象条件(如大气压力、干球温度及湿球温度)、淋水面积和风速等参数对冷却塔出塔水温的影响.即随着干球温度及湿球温度的降低,或者在一定的范围内,淋水面积的增大,或者风速的增大,出塔水温均会降低.结果表明:湿差模型和焓差三阶模型是适用于大型或超大型冷却塔的热力计算模型,在大型冷却塔设计时,应特别重视循环冷却水系统冷端参数的综合优化分析.关键词:大型冷却塔;热力计算;出塔水温;湿差模型;焓差模型;四变量模型中图分类号:TK123 文献标识码:A 文章编号:1000Ο1980(2009)05Ο0591Ο05冷却塔是火电厂的重要冷端设备之一,其冷却性能的好坏直接影响整个电厂运行的经济性和安全性.而冷
却塔的出塔水温是衡量冷却塔冷却性能的重要技术指标[1Ο4]
.根据冷却塔的出塔水温及其变化规律,不仅可以对冷却塔系统进行运行监控和状态优化分析,而且可以为冷却塔的运行维护和检修改造提供基本技术依据.
冷却塔的出塔水温对发电机组热效率的影响较大,如对于1台超高压汽轮机,当冷却塔出塔水温降低1℃,凝汽器真空提高270Pa,机组热循环效率提高012%~013%[5],因此,在冷却塔设计时首先必须采用准
确的热力计算模型.
在现行的冷却塔设计中,大多采用以麦克尔方程[6]为基础的焓差模型,即将接触散热和蒸发散热相关的2个未知变量(不同高度淋水截面的空气干球温度和空气中的水蒸气分压力)均用1个未知量“比焓”来代替进行热力计算,而很少用不同传质和传质系数的计算模型来计算.在焓差模型的求解上,则大多采用辛普森二阶积分法.但工程实践表明,这种以辛普森二阶积分的焓差模型(以下简称焓差二阶模型)不能准确地适用于目前的大型冷却塔[7](8500m2≤A<11000m2)以及超大型冷却塔(A≥11000m2)的热力计算分析,其中A为淋水面积.本文基于质量守恒和能量守恒原理,建立了适用于大型冷却塔热力计算的新的湿差模型,并与焓差二阶、三阶模型以及四变量模型分别进行了比较计算,分析了各有关参数对大型冷却塔出塔水温的影响.
1 湿差模型的推导
1.1 水体质量守恒方程
根据质量守恒原理,水面蒸发的水量,即部分变为空气中水蒸气的水量可表示为
dQ=βpv(p′v-pv)dV
(1)
式中:Q———进入冷却塔的水量,kg/s;V———填料体积,m3;βpv———单位填料体积与水蒸气压力相关的散质系数,kg/(m3・Pa・s);p′v———空气温度为水温t时的饱和水蒸气压力,Pa;pv———水蒸气的分压力,Pa.p′v,pv可
分别改写为
p′v=x′x′+01622pa
(2)pv=
xx+01622
pa
(3)
式中:x′———空气温度为水温t时的饱和蒸气含湿量,kg/kg;x———空气中水蒸气的含湿量,kg/kg;pa———大气压力,Pa.
将式(2)~(3)代入式(1),得
dQ=βxv(x′-x)dV=βxv(x′
-x)Adz(4)βxv=1161βpv[1-1161(x′
+x)]pa(5)
式中:βxv—
——单位填料体积与空气含湿量相关的散质系数,kg/(m3・s);A———塔中填料水平断面面积,m2;z———垂向坐标,向上为正.
由于空气中水蒸气增加的水量dQ也可以表示为
dQ=Gdx
(6)因此,由式(4),(6)可得
βxv(x′-x)Adz=Gdx(7)式中G为进塔空气质量,kg/s.
1.2 热量平衡方程
水散出的总热量为其水面接触散热量与其蒸发水量所引起空气温度增加的蒸发散热量的总和,即
dHq=αv(t-θ)Adz+γwβxv(x′
-x)Adz+ctdQ(8)
式中:Hq———水散出的热量,kJ/s;αv—
——单位体积接触散热系数,kJ/(m3・s・℃);t———水温,℃;θ———空气的干球温度,℃;γw—
——水的汽化热,取242813kJ/kg;c———水的比热容,取411868kJ/(kg・℃).空气增加的总热量为
dHg=Gcwdθ+hqdQ(9)式中:Hg———空气增加的热量,kJ/s;cw———湿空气的比热,取1105kJ/(kg・℃);hq———水蒸气含热量,kJ/kg.
在正常稳定运行状态下,水散发的总热量等于空气增加的总热量,则由式(8),(9)可得
αv(t-θ)Adz+γwβxv(x′
-x)Adz+ctdQ=Gcwdθ+hqdQ(10)考虑到蒸发水量dQ相对很小,将其带走的热量忽略,且hq=r0+cvθ,则式(10)可化简为
Gcwdθ=αv(t-θ
)Adz(11)
式中:r0———水0℃时的汽化热,kJ/kg;cv———水蒸气比热容,取11842kJ/(kg・℃
).1.3 热传递平衡方程
水损失的热量为
dHq=cQt-c(Q-dQ)(t-dt)
(12)式(12)为忽略二阶微小量化简得到的.将式(8)代入式(12),化简后可得
cQdt=αv(t-θ)Adz+γwβxv(x′-x)Adz(13)
令
GA=ga,Q
A
=q,将式(7),(11),(13)分别改写导出湿差模型即可:dxdz=βxv(x′-x)ga
(14)dθdz=α
v(t-θ)cwga
(15)dtdz=αv(t-θ)+γwβxv(x′-x)cq
(16)
求解式(14)~式(16)需作如下假设:(a)系数αv,cv,cw,c及γw都取常数;(b)水温取其断面平均值,不考虑交面阻力;(c)空气在填料出口处未达到饱和状态;(d)填料面积沿垂直方向不变;(e)取刘易斯数Le=
αv/(cwβxv)=111,1,0193,0191,019,分别计算其对出塔水温的影响.
2 焓差模型和四变量模型简介
2.1 焓差模型
水所损失的热量等于空气所获得的热量,即
cqdt=gadi
(17)
式中i为湿空气焓,kJ/kg.
从水到空气的热量传递,可用焓差[8]表示为
cqdt=βxv(i′
-i)dz(18)
式中i′为水温t时的饱和空气焓,kJ/kg.
将式(18)改写成积分形式,即
βxvz
q
=
∫
t1
t2
cdt
i′-i
(19)
求解式(19)需作如下假设:(a)水膜或水滴的表面温度与冷却水内部温度一致;(b)忽略蒸发水量损失;
(c)由于冷却塔内水蒸气的压力很小,对塔内压力影响很小,因此按照平均大气压来计算;(d)散热系数、散质系数和湿空气的比热在整个过程中均为常数.
对于式(19)右边项的积分,可采用辛普森展开法.当取辛普森阶数n=2,3时,可分别写成式(20),(21)的积分形式,本文分别称之为焓差二阶、三阶模型,即
∫
t1t2cdt
i′
-i=
cwΔt3n1h′2-h1+4h′m-hm+1h′1-h2(20)∫
t1
t2
cdt
i′-i=
cwΔt3n
1
h′2-h1
+
4
h′23-h13
+
2
h′13-h23
+
1
h′1-h2
(21)
式中:h1,h2———进塔、出塔空气比焓,kJ/kg;hm,h′m———塔内平均水温的空气比焓、饱和比焓;h13,h′23———空气干球温度为t=t2+1/3Δt时的比焓、饱和比焓,kJ/kg;h23,h′13———空气干球温度t=t2+2/3Δt时的比焓、饱和比焓,kJ/kg.2.2 四变量模型
根据质量守恒和能量守恒原理,并考虑蒸发损失引起的水量变化,可得四变量模型[6]:
dq
dz
=βpv(p′v-pv)(22)dt
dz=αvcq(t-θ)+γwβpvcq(p′v-pv)(23)dθdz=ccwgaqdtdz+1c(ct-γw-cθ)dq
dz
(24)dpv
dz=(pa-pv)201622gapadqdz
(25)
求解四变量模型需作如下假设[9]:(a)冷却塔内水蒸气分压力所占比例很小,可采用不变的大气压力;
(b)系数αv,cv,cw,c及γw都取常数;(c)水温取其断面平均值,不考虑交面阻力;(d)空气在填料出口处未达到饱和状态;(e)填料面积沿垂直方向不变.
3 4种模型的比较计算分析
现针对湿差模型、焓差二阶模型、焓差三阶模型、四变量模型这4种热力计算模型进行比较计算分析,并作如下说明:(a)湿差模型的求解,采用中心差分方法将偏微分方程组转化为差分方程组后再编写程序;(b)焓差模型的求解,分别对其二阶、三阶模型进行对比分析,同时为了保证式(20)的解有合理的求解区间曲
线[10],根据4个焓差都大于零的条件来编写Fortran程序,以使其解具有数学和实际意义;(c)四变量模型,采用中心差分方法将其转化为方程组后再进行求解,并考虑水量的蒸发损失.
本文以邯峰电厂冷却塔为研究对象.该冷却塔为自然通风冷却塔,淋水面积为9000m2,采用高为112m的T26Ο60°梯形波填料.气象条件为:空气干球温度2115℃,湿球温度17℃,大气压力99850Pa.
4种模型的热力计算结果如图1~4所示.比较分析这些计算结果,可得出如下结论:
a.四变量模型的出塔水温计算结果比其他模型大,与实测出塔水温比较误差较大,说明该模型相对不
准确.
b.由图1可见,当淋水面积从4000m2增大到8000m2时,焓差二阶模型的出塔水温计算结果与湿差模型的计算结果相差很小.但随着淋水面积的增大,焓差二阶模型的计算结果与湿差模型的计算结果相差越来
越大,此时,焓差三阶模型与湿差模型的计算结果越来越接近,且与实测出塔水温很接近.说明大型冷却塔的热力计算不宜再用焓差二阶模型,应采用湿差模型和焓差三阶模型.
c.由图2可见,随着风速的增加,出塔水温呈近似直线下降趋势.而由图3可见,随着冷却塔淋水密度的增加,出塔水温也相应增加.由图4可见:随着刘易斯数的增大,出塔水温减小;当刘易斯数从111减小到110时,出塔水温增加0115%.由此可见,刘易斯数的选取是值得注意的问题

大型冷却塔热力计算模型
上一篇:大型冷却塔的性能与选择
下一篇:大型冷却塔产品特点